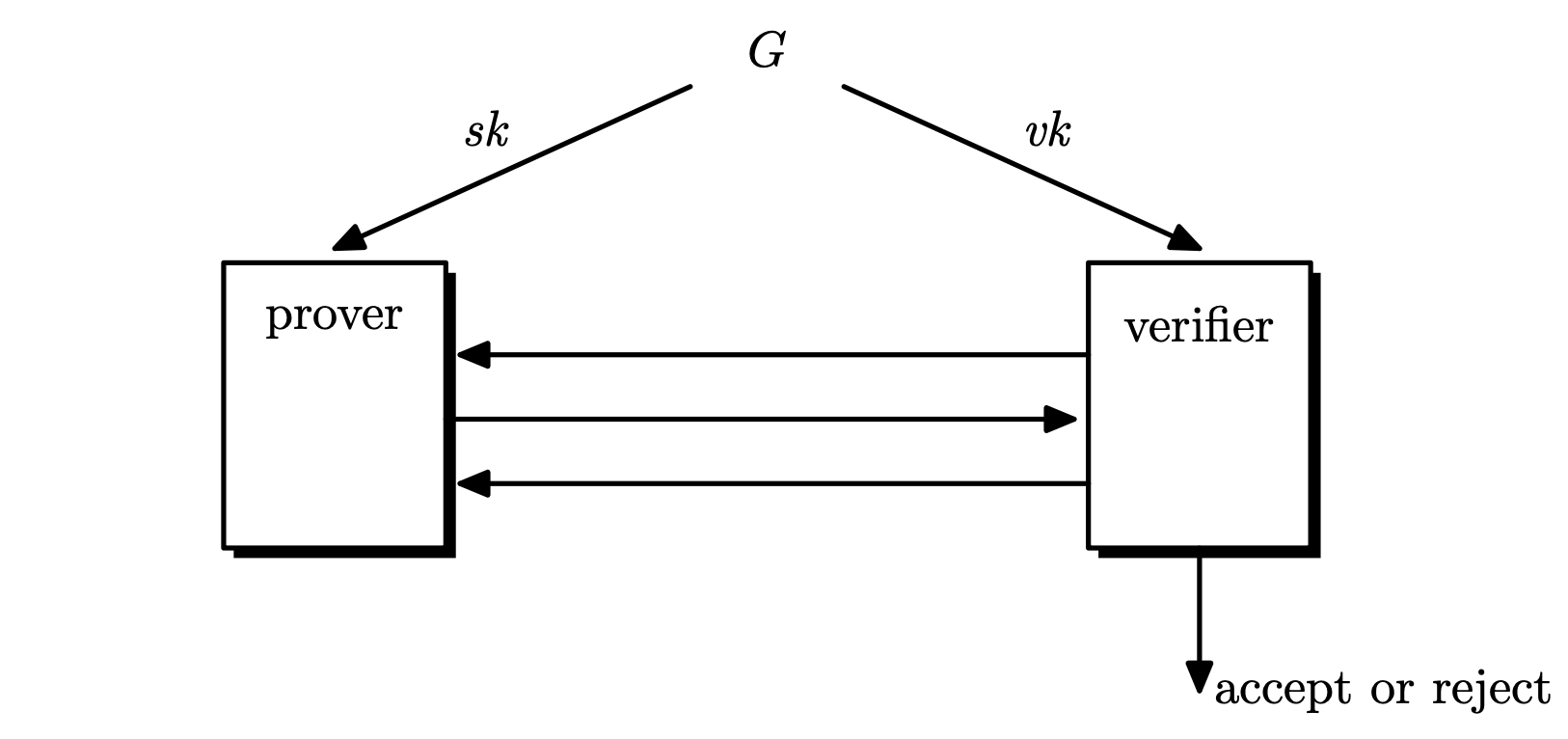
12. Zero-Knowledge Proof (Introduction)
In 1980s, the notion of zero knowledge was proposed by Shafi Goldwasser, Silvio micali and Charles Rackoff. Interactive proof systems: a prover tries to convince the verifier that some statement ...

In 1980s, the notion of zero knowledge was proposed by Shafi Goldwasser, Silvio micali and Charles Rackoff. Interactive proof systems: a prover tries to convince the verifier that some statement ...
중간고사 끝난 것을 기념으로! 근데 첫 문제는 시험 전날에 공부하기 싫어서 잡았다. 30323번 BOJ 30323: Exponentiation 주어진 $\alpha = x + x^{-1}$와 $\beta$에 대하여 $x^\beta + x^{-\beta} \pmod m$을 구하면 된다. 먼 옛날 곱셈 공식의 변형 [x^2 + \frac{...
Ciphertext Indistinguishability By Shafi Goldwasser and Silvio Micali Turing Award in 2012 An adversary should not be able to… (Semantic Security) gain any partial info...
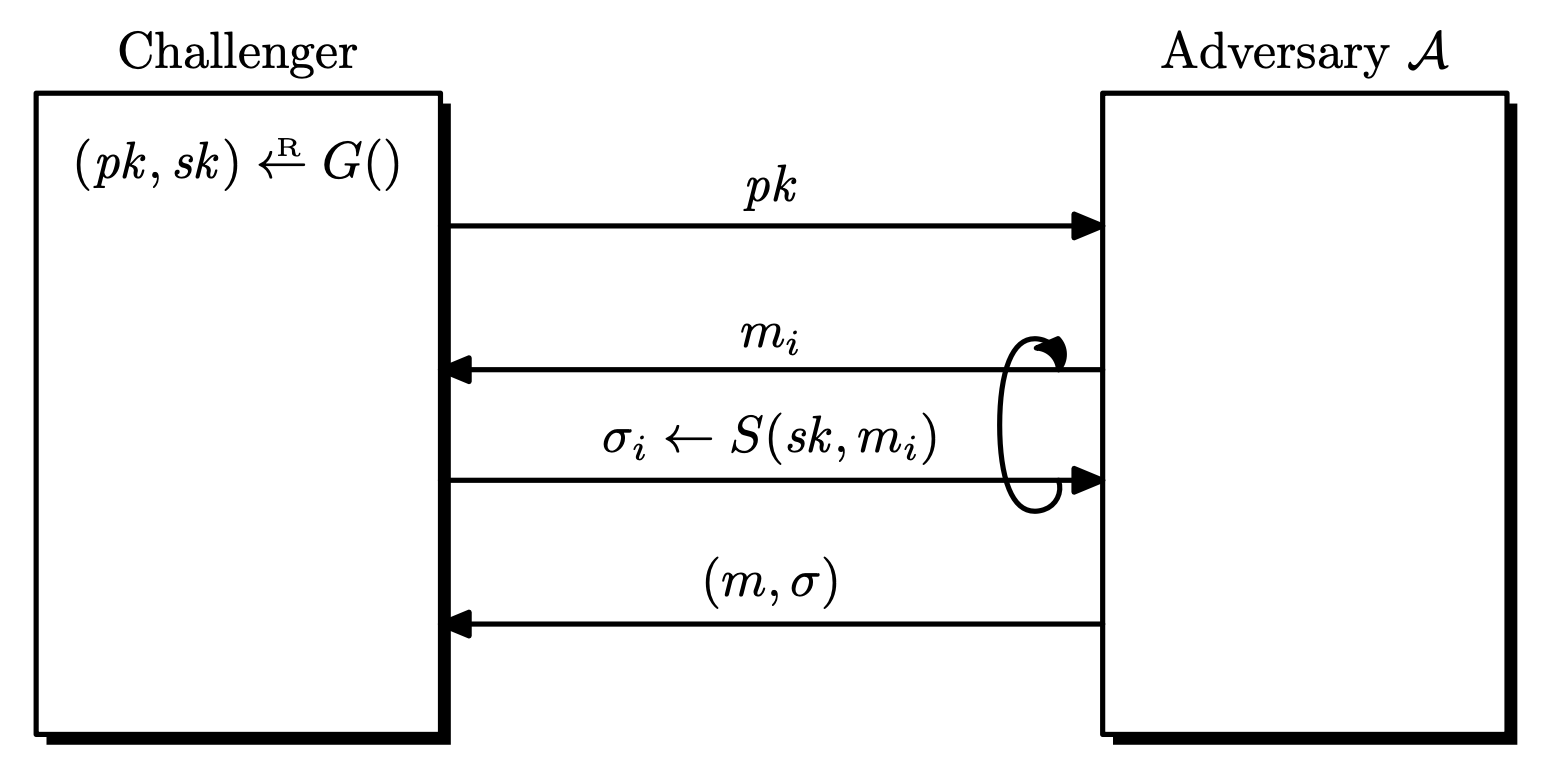
Digital Signatures Definition. A signature scheme $\mc{S} = (G, S, V)$ is a triple of efficient algorithms, where $G$ is a key generation algorithm, $S$ is a signing algorithm, and $V$ is a ver...
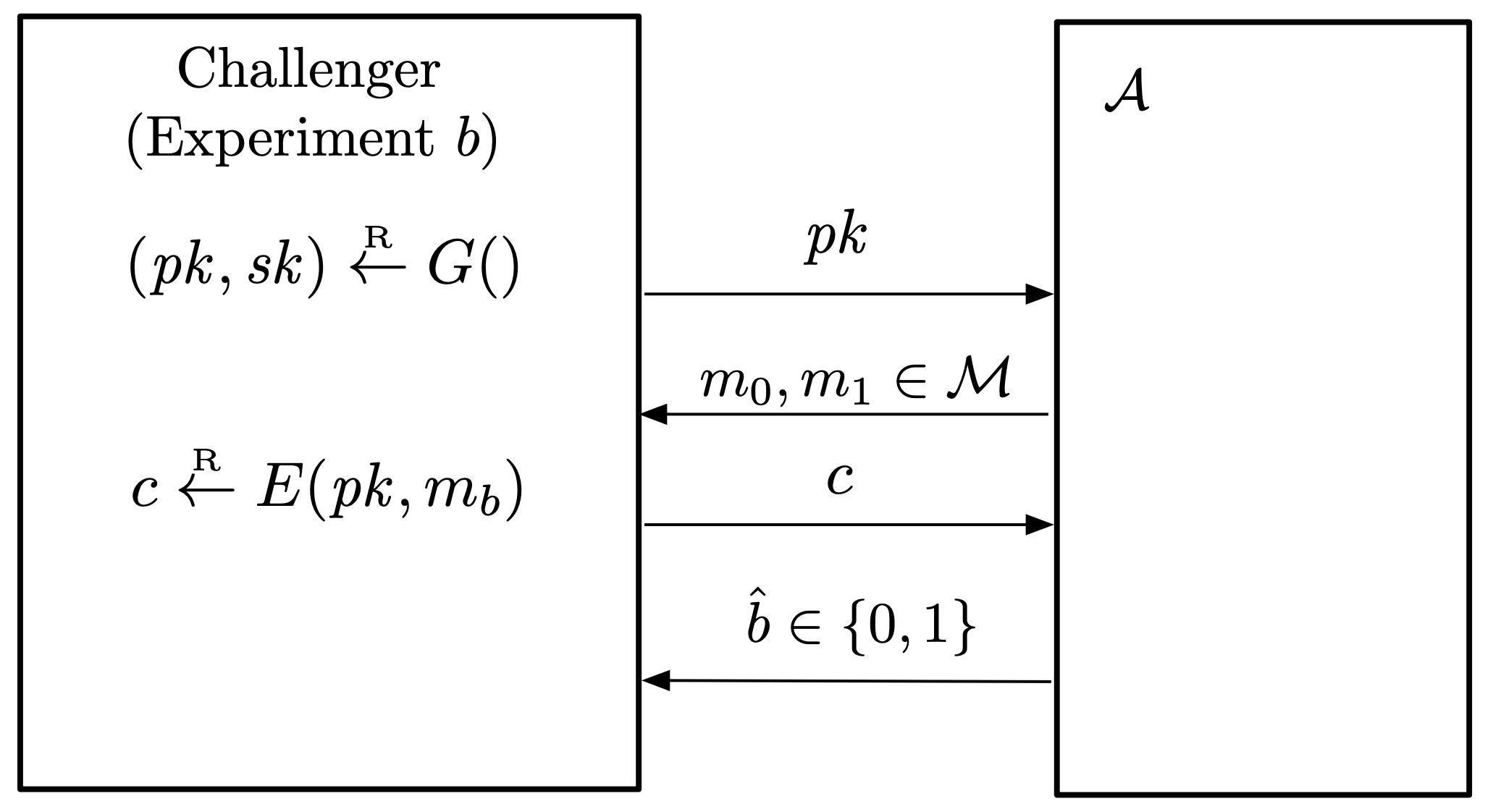
In symmetric encryption, we assumed that the two parties had a shared key in advance. If the two parties do not have a shared key, public-key encryption can be used to encrypt messages. Public Key...
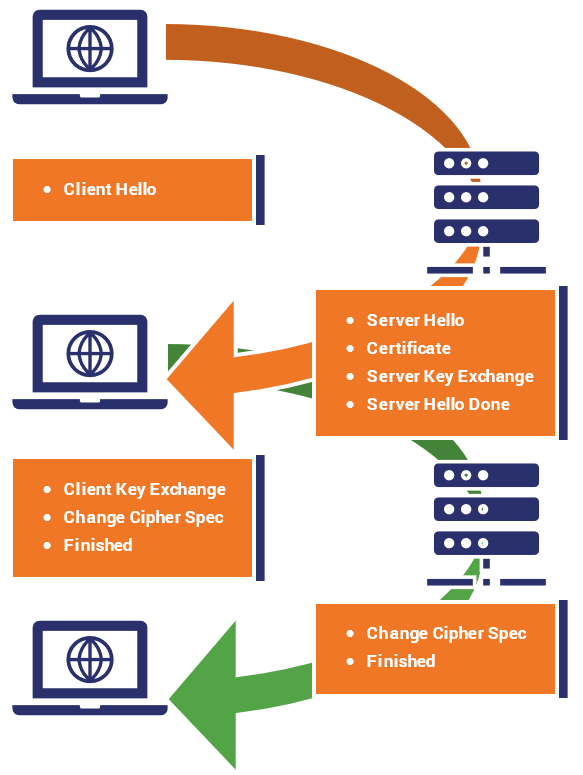
This is a brief comparison of HTTP and HTTPS HTTP: HyperText Transfer Protocol HTTPS: HyperText Transfer Protocol Secure Uses certificates, encryption, TLS. Used for privacy....
Suppose that we’re using RSA, Alice has public key $(N, e)$ and private key $d$. Anyone can send messages to Alice using $(N, e)$. But because anyone can generate $(N, e)$, we are not sure whether ...
In symmetric key cryptography, we have a problem with key sharing and management. More info in the first few paragraphs of Key Exchange (Modern Cryptography). Public Key Cryptography We use two k...
Background Number Theory Let $n$ be a positive integer and let $p$ be prime. Notation. Let $\mathbb{Z}$ denote the set of integers. We will write $\mathbb{Z} _ n = \left\lbrace 0, 1, \dots, n...
Exponential Inverses Suppose we are given integers $a$ and $N$. For any integer $x$ that is relatively prime to $N$, we choose $b$ so that [\tag{$*$} ab \equiv 1 \pmod{\phi(N)}.] Then we have [...